As discussed in Chapter 8, ozone amounts vary on many time scales. Some of these variations are cyclic in nature, such as the seasonal cycle and QBO, while others, such as El Nino episodes and dynamical variability, are less predictable. We know that all these processes effect ozone, but what we really want to know is the relative contribution of each process to the total variability of the ozone time series. Specifically, we want to know the magnitude of the long-term ozone trend. The key to calculating the trend is being able to separate it from other sources of variability. In fact, the uncertainty of the estimated trend is related to how well we have accounted for other sources of variability in our calculation. More will be said about uncertainty estimates is Section 4.0.
One way to separate the long-term trend from other sources of variability in the ozone time series is by constructing a statistical regression model. Regression analysis is a statistical technique that uses the relation between a dependent variable and one or more independent variables such that the dependent variable can be predicted by the independent variable(s) (e.g., Neter et al., 1985).
Example: consider Company X, which sells teddy bears. The number of teddy bears sold per day may depend on the price of each bear and the amount of money company X spends on advertising. In this example, the number of bears sold is the dependent variable, and the cost of each bear and amount of advertising money are the independent variables. When doing their bookkeeping, Company X will construct a regression model to determine the best mathematical relationship between the cost of each bear, the amount of advertising money spent, and the number of bears sold per day. They will base this model on trial cases where the company varied the cost of the bear and amount of advertising money spent, and monitored the change in the number of bears sold. Using these results, they can predict the number of bears that will sell at a particular price and level of advertising, and they can adjust these factors such that they meet their daily bear selling quota.
When a regression model includes only one independent variable it is know as a simple regression model; a multiple regression model includes more than one independent variable. In this study, we want to express the ozone variability in terms of the individual processes that cause the variability. We will construct a model where the dependent variable is the ozone time series and the independent variables are time series that represent the individual components of ozone variability, such as the seasonal cycle and QBO.
We know that some of the largest sources of ozone variability are the seasonal cycle, the QBO, the 11-year solar cycle, and the long-term trend. We can express the ozone time series as the sum of four independent time series; one representing the seasonal cycle, one the QBO, one the 11-year solar cycle, and one a long-term trend.
Quasi-Biennial Oscillation in Ozone + Long-Term Trend in Ozone + Residual
where the residual is the remaining unexplained variability of the ozone time series. These time series will become the components of our statistical model. To best determine the long-term trend component of an ozone time series, we must account for sources of variability on seasonal and interannual time scales. Short-term (day to day) variations have little effect on the statistical time series analysis used to estimate the long-term ozone trend.
We don't know the magnitude of each component yet, but we do know what each component looks like from other data sets. In Figure 9.03 for instance, Panel A shows the QBO in the equatorial zonal (i.e. from west to east) wind at Singapore, and Panel B shows the 11-year solar cycle in the 10.7 cm solar radio flux measurements.
We refer to these data as "proxies" for the model components, because each is used in the regression model as a proxy (i.e., as a substitute) for a particular component of variability. We assume a linear relationship between the proxy and the resulting variation of ozone. That is, we assume that the ozone response to each proxy has the same shape (i.e. time dependence) as the proxy itself. For example, the QBO in the Singapore wind time series has a period of about 29 months. Therefore, the model ozone QBO component will also have a period of about 29 months. For the seasonal cycle, we employ a combination of sine and cosine waves that repeat every year as the proxy. For the trend we assume a linear function of time as the proxy. This assumption is standard in current research, and is made for two reasons. First, the ozone observations, such as the Arosa Dobson data and TOMS satellite data presented in Section 2.0, show that a linear trend is a reasonable assumption. Second, and more importantly, the increase of CFCs released into the atmosphere, which is thought to be the physical cause of at least a portion of the observed trend, has also been generally linear during the 1980s (e.g., Montzka, et al., 1996). Therefore we are essentially using the increase of CFCs as the proxy for the long-term trend component in the model.
Note that the proxies we are using in this example are not the only possibilities. When deciding what to use as proxies for the components of ozone variability, we must use our knowledge about the different cycles of ozone to construct the most physically consistent model that we can. The better our proxies represent known variations of ozone, the lower the unexplained variability.
We now have all the pieces to construct our regression model. As stated above, we are using a linear function to relate each proxy to its corresponding component of ozone variability. Therefore, we use a linear regression model, in which the independent variable is expressed as a linear combination of the dependent variables. In a simple linear regression, the model takes the form of the equation for a line, y = m x + b. Here y is the dependent variable, x is the independent variable, m is the regression coefficient and b is the y intercept. The regression coefficient is the scaling factor between the dependent and independent variable, and the y intercept is simply the value of y when x = 0. For a linear multiple regression model, the equation has the more general form y = m1 x1 + m2 x2 + m3 x3 +...+ mnxn + b, where n is the total number of proxy terms in our model and b is the value of y when [x1, x2, x3, ..., xn] = 0.
In terms of our ozone model,
The time origin (t = 0) of the model is arbitrary, and in these examples is chosen to be January 1978. Therefore the constant term represents the model estimated ozone value in January 1978.
As an example, the QBO ozone component is expressed in terms of the assumed QBO proxy as
where the QBO proxy term (x3 above; as shown in Figure 9.03) gives us the shape of the QBO component, and C is a scaling factor (m3 above) that will tell us the magnitude and sign of the QBO component relative to the assumed QBO proxy.
If we expand each component in the same fashion, we can write our model equation for ozone variability as
Ozone= A * Seasonal Proxy + B * Solar Cycle Proxy + C * QBO Proxy +
D * Trend Proxy + Residual + Constant
We still need to include a term for the residual, or unexplained variability, because we know our model using the proxies for ozone variability will not exactly equal the observed ozone variability. We'll use the variance of the residual to determine how good or bad our model representation really is.
The variance of a time series is a measure of its variability. The variance is denoted by2, and is defined as
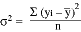
where yi is the time series value at the ith data point,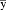
is the mean of the time series, and n is the number of data points in the time series. Since the residual has a mean value of zero, the equation for the variance can be simplified to
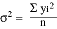
The unknowns in the model equation are the regression coefficients A, B, C, and D, the constant term (also sometimes considered a regression coefficient), and the residual. We will use the actual ozone time series to help us determine these coefficients. There are several statistical techniques to determine the regression coefficients. We use what is called a least squares technique. In this technique, the regression coefficients are determined such that the variance of the residual is minimized. In the next section, we'll demonstrate these techniques through some sample calculations. Further information on statistical regression analysis and least squares techniques is available in Neter et al. (1985) and most other textbooks on time series analysis (see suggested readings).
To demonstrate how linear multiple regression analysis is used, consider the global average time series of total ozone from the Nimbus 7 TOMS instrument (Figure 9.02a). The data are from November 1978 through May 1993 (when the TOMS instrument aboard Nimbus 7 ceased functioning).
Note: Throughout the remainder of this Chapter, we will be discussing ozone trend results. It is important to clarify some of the nomenclature before proceeding. For the most part, observed ozone trends in current research are negative, so we commonly use the absolute value of the trend to quantify its size. That is, when we refer to a larger trend, we mean that the trend value is a larger negative number. Conversely, smaller trends are less negative. By the same token, an increasing trend is becoming more negative, while a decreasing trend is approaching zero. It is helpful to keep this in mind when interpreting the trend results that follow.
3.3.1 Estimating long-term ozone trends using a simple linear regression model -- First we construct a simple linear regression model with only one model component, the long-term trend. That is,
In this case, all the other ozone variations, such as the seasonal cycle and QBO, are included in the residual. In this simple model, these sources of variability are unexplained. If we assume time as our proxy for the long-term trend, as discussed in the previous section, we can rewrite this equation as
where D is the regression coefficient (we choose "D" as the variable name for consistency with the previous model equations) and Constant is the estimated value of the ozone at the designated reference time t = 0, January 1978 (see Figure 9.04a).
Referring back to the general equation for a simple linear regression model, y = mx + b, y = ozone; x = time; m = D, and b = Constant. The regression coefficient D is our trend term.
Figure 9.04a shows the globally averaged ozone time series (same as in Figure 9.02a) with our best fit linear trend component drawn in as the solid red line. Constant is denoted by the dashed purple line in this figure. Figure 9.04b shows the model residual in blue, with the trend uncertainty range denoted by the dashed red lines (see discussion below). Some important points in Figures 9.04a and b are
level. The uncertainty is a statistical measure of how certain we
are that the calculated trend equals the real trend in the data.
The 2
uncertainty level means that there is a 95% chance that the real
trend lies between the two dashed lines [-3.33% per decade and
-1.07% per decade].3.3.2 Estimating long-term ozone trends using a multiple linear regression model -- In this section, we will investigate other sources of variability in the ozone. By constructing a model with components for other sources of variability, we expect to reduce the uncertainty of the trend estimate derived in the previous section. To demonstrate, we will construct several models, each with one additional component.
If we again return to the original time series (Figure 9.02a), we see that the clearest cycle in the data is the seasonal cycle. So we'll construct a model with only a seasonal cycle component.
We'll use a combination of sine and cosine waves for the seasonal proxy. The reader might recall from trigonometry that any function may be expressed as the liner combination of sine and cosine waves with different periods. The ozone seasonal cycle has a relatively simple structure, and can be reproduced by adding only a few sine/cosine waves with periods that are an integral factor of 12 months. For details on the mathematical form of the seasonal proxy, see A in the Bonus Information section. Note that the residual Res1 for this model is not the same as the residual for the previous model. The constant term also changes each time we add a component, but it always represents the model estimated ozone value at time t = 0.
Using a least squares technique to solve for all the constants (A,Con1), we get the red dotted line in Figure 9.05a Panel A as our estimated global ozone seasonal cycle.
The solid blue line in Panel B of Figure 9.05a is a plot of the residual, Res1, which is the variability unexplained by the seasonal cycle. [For clarification in the plots, the residual is shifted downward slightly. The actual mean of the residual is always zero.] Note that in this residual plot we see a component of variability that looks very much like the solar cycle we saw in Figure 9.04, the 10.7 cm solar radio flux.
To model the solar cycle, we add a solar component to the model.
where Solar Cycle = B * 10.7 cm Solar Radio Flux, assuming the 10.7 cm solar radio flux as the proxy for the solar cycle of ozone. We derive the solar cycle component, as shown by the red dotted line in Figure 9.05a Panel B, by solving for the new set of regression coefficients (A, B, and Con2).
Panel C of Figure 9.05b shows the remaining variability (Res2; solid blue line) not accounted for by the seasonal or solar cycles. After we have accounted for the solar cycle variability, we can see peaks in the data about every 2.5 years. This is indicative of the QBO signal, as seen in Fig. 9.05a Panel A. We therefore include a QBO component:
where QBO = C * 30 mb Singapore zonal wind, assuming the 30 mb Singapore zonal wind as the QBO proxy. As before, by solving for the new set of regression coefficients (A, B, C, and Con3), we derive the QBO component. Figure 9.05 Panel C also shows the estimated QBO component as the red dotted line.
The solid blue line in Figure 9.05b Panel D shows Res3, the component of ozone not accounted for by the seasonal, solar, or QBO cycles. We've now removed all the major sources of variability except the long-term trend. However, there are still some sizable variations about the systematic decrease in the ozone. Most notably, the lowest ozone values tend to occur in the winter of each year. Therefore, instead of fitting a simple linear function, we fit a trend that varies with season. That is, the estimated winter trend value may be different than the estimated summer trend value. We call this our long-term, seasonally varying trend (not to be confused with our seasonal component).
Our final model is therefore
Long-Term, Seasonally Varying Trend + Res4 + Con4
where Long-Term, Seasonally Varying Trend = D(t) * Time.
In this case, the regression coefficient D varies with time. As with the seasonal cycle, we use sine and cosine waves to characterize the seasonal variations. See Bonus Information, B, to see the exact functional form of the seasonally varying trend proxy.
The estimated seasonal trend is shown as the red dotted line in Figure 9.05b Panel D. Much of the remaining variability in Res3 (blue line) can be represented by the seasonal trend component.
We have just constructed a statistical model to estimate the long-term trend in the global ozone time series and account for some of the other known sources of variability in the data. Figure 9.05c Panel E shows the final residual, Res4 (blue line). This unexplained variability is used to estimate the trend uncertainty.
When we did not include any components other than the linear trend in our model, the trend estimate was -2.2% per decade, and the estimated uncertainty of the trend was ±1.13% per decade. With the inclusion of the other model components, the estimated trend is -2.04% per decade, and we have reduced the trend uncertainty to ±0.28% per decade. Note that trend value itself changed slightly. This is because a small portion of the simple trend we calculated was actually a result of the other sources of variability. In a statistical sense, we are much more confident that this trend value is close to the "true" trend.
3.3.3 Remaining unexplained variability -- With our full model, we've done a good job of reducing the unexplained variability in the global ozone time series. Some large-scale variations still remain. If we could model these variations, we could reduce the trend uncertainty even more. As discussed in the Ozone Variability chapter (Chapter 8), there are many other processes which may affect ozone, including volcanoes, El Niño Southern Oscillation (ENSO), and dynamical processes. Many researchers in the field of ozone science are currently working to develop proxies which are representative of these processes, to construct models that better fit the data. However, because less is known about these sources of variability, developing the appropriate proxies for the statistical model is not an easy process.
Using a statistical regression model with terms for the seasonal cycle, Quasi-Biennial Oscillation (QBO), 11-year solar cycle and seasonally varying long-term trend, we can separate an ozone time series into its prescribed components. Figures 9.06a-d show the results of such a calculation using Nimbus 7 TOMS total ozone data in four latitude bands: (a) 30-50°N; (b) 30-50°S; (c) Equator-10°N; and (d) 60°N-60°S. Each figure shows the original ozone data, and the estimated components. The solid purple line in the top panel denotes the actual ozone data time series. The constant term, given by the purple dashed horizontal line in the top panel, represents the model ozone value in January 1978. Note that we don't have any actual data in January 1978, so the constant term is an extrapolation of the data. If we were to add the constant term, the seasonal cycle, the QBO, the solar cycle, and the long-term "seasonal" trend components, we would get the model ozone, shown by the red dotted line in the top panel of each figure. The model ozone is close to, but not exactly the same as, the data. The remaining panels show, in descending order, the seasonal, the QBO, the solar, the long-term trend and the residual terms. The residual is the difference between the model ozone (the sum of the components) and the actual data (solid purple line in top panel).
We note several features in each of the model components. Physical explanations for the sources of these features can be found in previous Chapters.
3.4.1 Seasonal cycle -- Comparing the seasonal cycle component (blue curve) in each figure, we note the following points.
3.4.2 Quasi-biennial oscillation -- Comparing the QBO component in each figure (green curve), we note the following points.
3.4.3 Solar cycle -- Comparing the solar cycle component in each figure (yellow curve) we note the following point.
3.4.4 Long-term, seasonally varying trend -- Comparing the seasonally varying trend component in each figure (orange curve) we note the following points.
A more detailed description of results from ozone trend research is presented in Section 5.0.
|
|
 |
|
